Pathfinding
This is a collection of thoughts, documentations, mumbling, and explanation of the work done about pathfinding. Any ideas or comments are more than welcome.
Up to now, only KotOR and nwn have been investigated. Any "findings" might not apply to other games.
How pathfinding works?
The engine seems to use a navigation mesh or walkmesh as the underlying data structure. It is simply a polygon mesh where each face has a walk property to state if an agent/creature can walk on this particular face and what kind of material the face is (metal, carpet, grass,…).
A* algorithm
The first step in pathfinding, is to find a series of adjacent faces among the navigation mesh that constitutes a path between two points. Ideally, the path is the shortest one but it highly depends on the quality of the walkmesh and the kind of algorithm used. As we want to reuse what is already there – the walkmesh – our only leverage will be the algorithm part though some pre-processing steps on the walkmesh might be needed as explained later.
There are several algorithms that tries to achieve that goal. A* and all its variants is a widely used algorithm in games and real-time applications, it is both accurate and fast though it won’t necessarily give the best path but one of the bests. Basically, it will start from an endpoint of the path and try to go around, on another face, and estimates if it is closer to the other side of the path. The main area one can improve about the algorithm’s performance is on the way it thinks how closer it moves to the end. The function that gives this estimation is called the heuristic and will be discussed later.
Simple Stupid Funnel Algorithm
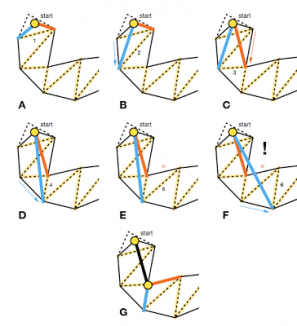
Once we have a series of adjacent faces, comes the second step: to have a nice line our creature can follow. Again, there are several algorithms able to address that kind of issue, though I will focus on the Simple Stupid Funnel Algorithm(SSFA) taken from Mikko Mononen blogpost and author of the Recast and Detour toolset. The idea behind SSFA, is like pulling two strings from the start to each border of the faces path. The algorithm goes from vertex to vertex that belongs to the border and must make the funnel formed by the two strings narrower at each iteration and lie inside the faces path. Otherwise, it has to pull the strings from a previous vertex. As an image is worth a thousand words:
On the above image, A-B-C-D steps narrow the funnel. In the E step, the red string cannot move since it would be outside the path. In the F step, the two strings are crossing so it has to restart from a previous vertex in the next iteration i.e. the G step.
One thing that SSFA doesn’t directly take into account is creature’s size. In deed, it gives us a path that sticks to the border. To deal with it, one trick[1] is to consider a circle around each vertex that cannot be crossed by the funnel.
Other steps
While we can have a beautiful an acceptable path with A* and SSFA algorithms, the job is far from being done. First, the walkmesh doesn’t take into account all static objects like crates or seats. Somehow, some of those static objects are included in the walkmesh and some don’t (screw you bioware!). An idea to deal with that, would be to add those static objects to the walkmesh directly as a pre-processing step or simply consider them as dynamic objects.
Anyway, pathfinding also have to handle dynamic objects i.e. the ones that can move, be destroyed or spontaneously appear. Contrary to the previous steps, this needs to be done along the path a creature is taking. I guess it should be independent from A* and SSFA and done by scanning with rays or something else what’s in front of the creature in real-time.
Show me the code!
A first proof of concept has been made in this branch. It is an awful code with lot of dead code and stuff nobody should ever see. It only works (A* and SSFA) with KotOr but has some code for nwn. Also, it needs Boost.Geometry to run. Let’s try to explain the code in details and the choices made.
General considerations
3D vectors
Both algorithms extensively use 3D vectors and related operations. Should we use Common::Vector3 generally or only when it is really needed and uses arrays for all the other cases?
Walkmesh data format
KotOR
Nwn
A* Algorithm
Though each game comes with it's own walkmesh dataformat, at the end we need an underlying structure that will store the walkmesh. In the POC, the walkmesh is stored in 5 std::vector:
- A vector of float which contains the vertices,
- A vector of
UINT32for each face of the walkmesh. It stores the related vertices and thus is three times the total number of faces (which are triangles). - A vector of
UINT32for adjacent faces. It stores for each side of a face, the adjacent face.UINT32_MAXis used when there is no adjacent face. - A vector of
UINT32for face property. It stores the kind of material the face is. - A vector of AABB trees. Each leaf of an AABB tree embeds a face. This allows to make fast face search based on coordinate.
Graph structure
A* is graph based algorithm with nodes and edges. Different choices can be made on what nodes and edges are. Vertices and faces can be taken as nodes as well as a side of a face, the edges being what connects them. For simplicity sake, in the POC, face has been taken as node and face adjacency as edge. Other choices could lead to better or worst performances as regards of the length of the path and time spent.
Open list
A* uses a priority queue to perform the repeated selection of minimum (estimated) cost nodes to expand [Wikipedia]. The POC uses a std::vector which is sorted whenever a node is added. This is obviously not the fastest way to do it. std::priority_queue could be used as well as boost.heap which is, imho, more complete. Though performance drops might only appear with big/complex walkmesh.
Estimation and heuristic function
The total estimation when A* tries to find the best next node, is given by the sum of two functions. The current cost function that gives the current length of the path. and the heuristic function that estimates the length to the end. In the POC, the former is measured by the path going through the middle of each edge it crosses (as seen in #A* algorithm). This could obviously changed, one can take the center of a face/triangle (incenter, centroid, …) for instance. The more naive heuristic function is simply the direct length to the endpoint. Again this could be improved in some specific cases, as the walkmesh is built from several parts (tiles, rooms,…), one can directly run A* on those by considering them as one big face. It could be a real improvement in maze like areas.
Creature's size
This is an ideal step to check if the creature will fit into the path. In the POC, each face A* tries to go is naively checked by the size of the crossing edge. If it is too small, a second check is done by looking the intersection between a segment the size of the creature and the faces around. The first check might get false-positive with flat triangles and something else should be considered like in [1].
External libraries
Several geometric functions are needed to make everything work (intersections between different polygons, distances,…) though most of them in the POC are home-made/based on google results, some use Boost.geometry (at least one) for simplicity sake. I guess, we should use this library as most as possible from a maintenance, efficiency and performance perspective. There is also CGAL that seems complete though it didn't convince me at first sight.
Simple Stupid Funnel Algorithm
The SSFA is relatively straightforward technically. The main difficulty is about creature's size. In order to take it into account, the POC computes tangents between the circles around vertices.
References
[1] Efficient Triangulation-Based Pathfinding, Douglas Demyen and Michael Buro.